Are Schools (Cognitively) Nutritive for Children’s Complex Thinking?

Today we host a very stim­u­lat­ing essay on the impor­tance of prob­lem-solv­ing and encour­ag­ing com­plex game-play­ing for chil­dren’s com­plete “cog­ni­tive nutri­tion”. Enjoy!

——————–

Chil­dren’s Com­plex Thinking

– By Tom O’Brien and Chris­tine Wallach

Pop over to your neigh­bor­hood school and vis­it some class­rooms. Is what’s hap­pen­ing cog­ni­tive­ly nutri­tive? That is, does it sat­is­fy present needs and pro­vide nour­ish­ment for the future health and devel­op­ment of chil­dren’s thinking?

Or is it puni­tive, with lit­tle con­cern for present nour­ish­ment and future health and development?

The Genevan psy­chol­o­gist and researcher Her­mi­na Sin­clair said, 

All of us con­cerned with edu­ca­tion should view chil­dren as wear­ing sign­boards say­ing Under Con­struc­tion. No, wait a moment. I did­n’t say that strong­ly enough. All of us should look at peo­ple as wear­ing sign­boards say­ing, Under Con­struc­tion — Self Employed. (See Ref­er­ence 1.)

We are in the fifth year of research, work which sheds light on Sin­clair’s claim, shows that present edu­ca­tion­al goals for chil­dren are often triv­ial, and which sug­gests that cur­rent meth­ods of caus­ing learn­ing to take place should be re-thought.

The work shows that chil­dren at grades 1–5 are capa­ble of stun­ning­ly com­plex think­ing and that this goal can be achieved with no direct teach­ing, but rather by pos­ing prob­lems for the chil­dren to solve.

Our work involves casu­al log­i­cal games cre­at­ed by O Brien. Reports on the research appear in Ref­er­ence 2.

The games are avail­able for Palm pdas through OS 5 at Handango.com under the title Trea­sure Hunt. See Ref­er­ence 3.

The games involve a search for jew­els on a 4 by 4 grid.

In all games, play­ers ask for infor­ma­tion and then assess the con­se­quences of the infor­ma­tion to locate the jewel(s) with log­i­cal neces­si­ty. The issue is infer­ence: the deriv­ing of new infor­ma­tion (con­clu­sions) from old infor­ma­tion (data).

In all games, two lev­els are avail­able: 1) search for 1 jew­el and 2) search for 2 jewels.

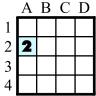
In one game, Find the Emer­ald, an emer­ald is hid­den at ran­dom and the play­er choos­es a box (in this case, A‑2.)The dis­tance from A‑2 to the mys­tery jew­el is 2. The dis­tance is left-right and up-down, not diag­o­nal. So if a child asked about A‑2 and if the feed­back were 2, the Emer­ald would have to be in B‑1, C‑2, B‑3, or A‑4. Which box would you ask about next?

In a dif­fer­ent game in the Trea­sure Hunt suite, Rubies, play­ers choose a box and the com­put­er looks in that box and all the box­es which touch that box and tells the play­ers whether or not it sees a Ruby. (In the case of the two-Ruby game, the com­put­er reports 0, 1 or 2 Rubies seen.)

In a third game, Dia­monds, the play­er choos­es a box. If the mys­tery jew­el is in that box or if it is touch­ing that box side­ways, the feed­back is Hot. If the mys­tery jew­el is touch­ing the child’s box cor­ner­wise, the feed­back is Warm. If the two box­es are not touch­ing, the feed­back is Cold. (In the two-Dia­mond game, the child’s box may be Hot to one jew­el and Warm to anoth­er. The feed­back is Hot, because Hot over­rules Warm. Sim­i­lar­ly, Hot over­rules Cold. And Warm over­rules Cold.)

Dur­ing our research, no teach­ing took place aside from giv­ing chil­dren an expla­na­tion of the rules of the game. Chil­dren worked togeth­er with the teacher as the data-giv­er. Some­times a Palm device and a pro­jec­tion device were used and some­times the teacher cal­cu­lat­ed the feed­back and record­ed the data on a chalkboard.

Although three-jew­el games have not been pro­grammed for the Palm, recent research has involved three-jew­els (with the teacher hid­ing the jew­els and cal­cu­lat­ing the feedback.)

One-jew­el games are acces­si­ble to most chil­dren, even as ear­ly as grade 1. Two- and three-jew­el games, how­ev­er, are very com­plex. Read­ers are encour­aged to play the games with friends with or with­out an elec­tron­ic device.

Con­clu­sions

The main find­ings were four:

1. In gen­er­al, chil­drens think­ing from grade 1 to grade 5 was very com­plex and eco­nom­i­cal. Chil­dren very rarely asked a use­less ques­tion and very rarely made a false inference.

2. Chil­dren worked togeth­er with enthu­si­asm and respect. They ques­tioned each oth­er’s think­ing in ways that were con­sid­er­ate, and they sup­port­ed each oth­er’s learn­ing by explain­ing how they arrived at their con­clu­sions. This behav­ior would be a sur­prise to many teach­ers. How to explain what hap­pened? Chil­dren were trust­ed to tack­le very com­plex tasks rather than being spoon fed with the accom­pa­ny­ing hid­den mes­sage, “You are capa­ble only of fol­low­ing the teacher’s instructions.

3. Vir­tu­al­ly all chil­dren were suc­cess­ful­ly engaged and it was often the case that chil­dren who had had lit­tle class­room suc­cess did very com­plex think­ing. One impli­ca­tion is that the tra­di­tion­al method, direct teach­ing, often does­n’t encour­age orig­i­nal and com­plex think­ing Our research shows that they crave it.

One girl who was birth-deformed and who nev­er spoke above a whis­per, took over the class at one point, “Tell me, John, What box do you want to know about? A‑3? A‑3 is 3. What are the con­se­quences? Now, Susan, tell me what you have to add to what John just said. Anoth­er child, Boris, had had no suc­cess, aca­d­e­m­i­cal­ly or social­ly, from kinder­garten to grade 5. He thrived on the search games. Unknown to the school staff, Boris was an Asperg­er’s log­ic machine, capa­ble of incred­i­bly com­plex thinking.

4. Through­out the years of research, evi­dence has been pre­sent­ed to sup­port the view that learn­ing involves pro­voked adap­ta­tion. Peo­ple revise their orig­i­nal net­works of ideas and con­struct new ones in the face of chal­lenges, nov­el­ty and prob­lem sit­u­a­tions. This is far from what’s com­mon­place in today’s world of fun­da­men­tal­ist abso­lutist author­i­tar­i­an poli­cies and practices.

Com­ments

The notion that knowl­edge is con­struct­ed is not pop­u­lar in these days. Indeed, a denial of this fun­da­men­tal human act per­haps the must fun­da­men­tal cog­ni­tive act of all has led Amer­i­can edu­ca­tion­al crit­ics to impose an approach to edu­ca­tion appro­pri­ate only for par­rots. See Ref­er­ence 3.

But in our research one sees chil­dren con­struct­ing impor­tant ideas con­cern­ing log­i­cal necessity.

The research sup­ports the idea that knowl­edge evolves in terms of coher­ence, sta­bil­i­ty, econ­o­my and gen­er­al­iz­abil­i­ty. And when it achieves equi­lib­ri­um it quests.(See Ref­er­ence 4. It was rou­tine no, uni­ver­sal that kids fin­ished a game and said, “Can we do a hard­er one?”

Are these expe­ri­ences nour­ish­ing? That is, will they have an effect twen­ty years from now? We don’t know. Come back in twen­ty years.

We think that the answer is yes. We base this hunch on the fact that we meet par­ents in the school­yard or the gro­cery sto­ry who say, “What are these log­ic games John­ny is play­ing in class? He likes them very much and he has the whole fam­i­ly play­ing Emer­alds and Rubies and Dia­monds around the din­ner table at night.”

Oth­er kids pop back to class two or three years after their class has moved on. “Can I play Dia­monds? I remem­ber the game well.” And they play a game or two of Dia­monds with all their tac­tics still fresh.

Indeed, it is the rare teacher who can cite such events. Rather, they say, “With the tra­di­tion­al cur­ricu­lum it often seems as though that kids for­get every­thing they’ve learned when sum­mer vaca­tion arrives. They come back in Sep­tem­ber hav­ing for­got­ten near­ly every­thing. It seems like they had nev­er been to school in the first place.

— Thomas C. O Brien is pro­fes­sor emer­i­tus, South­ern Illi­nois Uni­ver­si­ty at Edwardsville. He is a for­mer North Atlantic Treaty Orga­ni­za­tion (NATO) Senior Research Fel­low in Sci­ence. He is a con­sul­tant, author, and soft­ware devel­op­er. His web­site is http://www.professortobbs.com/.

— Chris­tine Wal­lach is a vet­er­an teacher at New City School, St. Louis MO.

Ref­er­ences

1. Extracts from a Sem­i­nar, “Intel­lec­tu­al Devel­op­ment, Research and Edu­ca­tion,” by Her­mi­na deZwart Sin­clair (Uni­ver­si­ty of Gene­va), Teach­ers’ Cen­ter Project, South­ern Illi­nois Uni­ver­si­ty at Edwardsville, Edwardsville, IL, 1977.

“The Child as Sci­en­tist,” an inter­view with Her­mi­na deZwart Sin­clair (Uni­ver­si­ty of Gene­va), Teach­ers’ Cen­ter Project, South­ern Illi­nois Uni­ver­si­ty at Edwardsville, Edwardsville, IL, 1977.

2. Thomas C. O Brien and Judy Bar­nett, “Fas­ten your seat belts,” Phi Delta Kap­pan, 85(3), 201–6, Novem­ber 2003.

Thomas C. O Brien and Judy Bar­nett, “Hold on to your hat,” Math­e­mat­ics Teach­ing, 87, June 2004.

Thomas C. O Brien and Chris Wal­lach, “Chil­dren Teach a Chick­en,”  Math­e­mat­ics Teach­ing, 93, Decem­ber 2005.

Thomas C. O Brien, “A Les­son on Log­i­cal Neces­si­ty,” Teach­ing Chil­dren Math­e­mat­ics, 13(1), August 2006.

Thomas C. O Brien and Chris Wal­lach, “Chil­drens Con­struc­tion of Log­i­cal Neces­si­ty, Pri­ma­ry Math­e­mat­ics, Autumn 2007.

3. The Trea­sure Hunt games are avail­able for pur­chase at www.Handango.com. See Here.

Two oth­er suites of O Brien’s soft­ware, Find It and Mys­tery Three, show iden­ti­cal research results, These can be found at the Han­dan­go site.

Accord­ing to Palm experts, all three soft­ware suites work with all mod­els of Palm devices includ­ing hand­helds and smart phones  i.e., M100 series, M500 series, Lifedrive, Tung­stens, Zires, Tre­os and Centro.

4. Thomas C. O’Brien, “Par­rot Math,” Phi Delta Kap­pan, 80(6), Feb­ru­ary 1999.

5. Thomas C. O Brien, “What’s Basic a Con­struc­tivist View” in Hand­book of Basic Issues and Choic­es, Nation­al Insti­tute of Edu­ca­tion, USOE, March 1982.

Thomas C. O Brien, “Some Thoughts on Trea­sure-Keep­ing,” Phi Delta Kap­pan, Jan­u­ary 1989.

Thomas C. O’Brien, and Ann Moss, “What’s Basic in Math­e­mat­ics?,” The Prin­ci­pal, Novem­ber 2004